标签：算法 - 莫小白

常见排序算法可以分为两大类：
非线性时间比较类排序：通过比较来决定元素间的相对次序，由于其时间复杂度不能突破 O(nlogn)，因此称为非线性时间比较类排序。
线性时间非比较类排序：不通过比较来决定元素间的相对次序，它可以突破基于比较排序的时间下界，以线性时间运行，因此称为线性时间非比较类排序。

算法复杂度

1. 冒泡排序 (BubbleSort)

冒泡排序是一种简单的排序算法，是一种减治算法的应用, 通过重复走过要排序的数组，每一次比较两个相邻元素的大小，如果后一个元素比前一个元素小就交换过来，最终完成排序，这种算法的命名也是由最小的元素总是会慢慢从最后 “浮” 到前面来而得名 (每次从无序区间取一个数去无序区间遍历)

步骤：

从第一组两个相邻元素开始比较，依次往后交换
每经过一次排序较大的元素就会被放到后面，直到最大的元素被放到最后，那么下一次排序的时候也就不用用它（最后一个数）和它相邻的前面的数进行比较了，最后的元素就成了 “稳定元素”
重复以上步骤，每一次排序完成，最后的 “稳定元素” 都会增加一个，直到没有可以交换的元素，那么排序就完成了

** 动态图演示：**

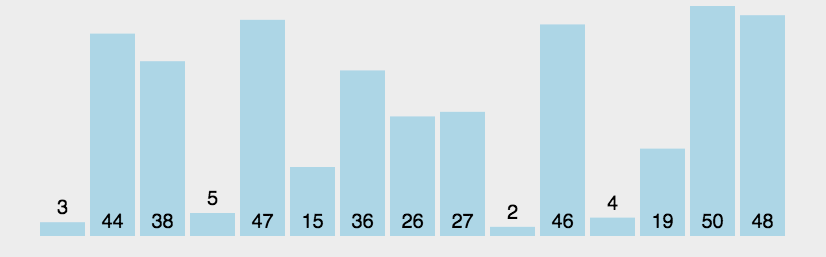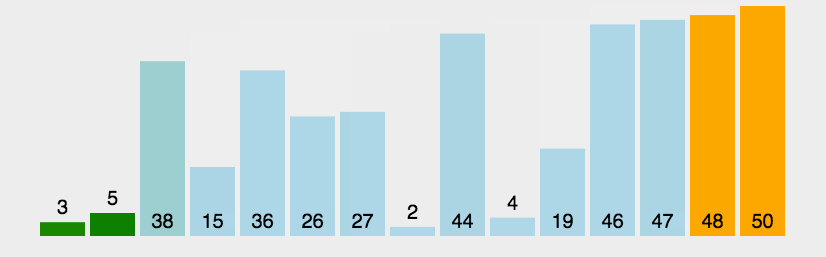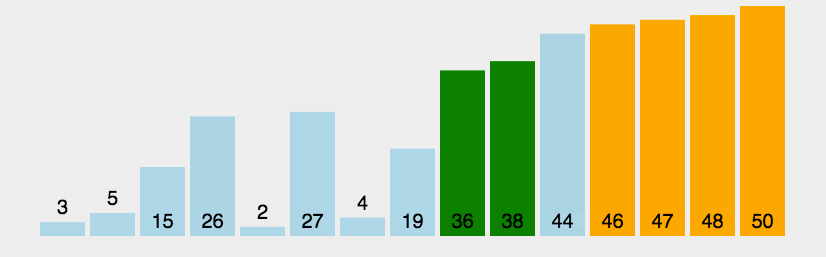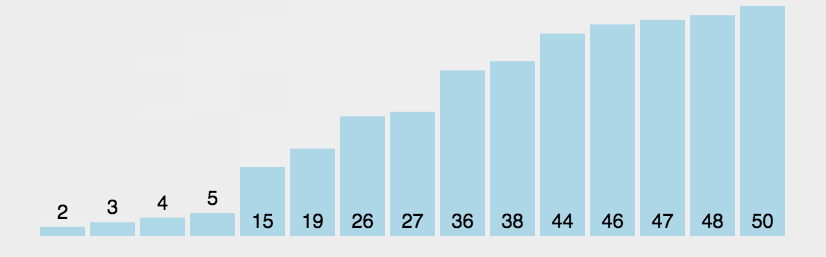
** 代码展示**

package com;

import java.util.Arrays;

/**
 * package:com
 * Description:bubbleSort
 * @date:2019/4/27
 * @Author:weiwei
 **/
public class bubbleSort {
    /**
     * 双层循环遍历数组
     * 第一层循环表示循环次数,一次循环解决一个数的问题,一共需要array.length次
     *       更优化的方式是array.length-1次(最后一个数不需要比较)
     * 第二层比较相邻两个数的大小,共需要array.length-2-i次(i是循环到哪个数,2是最后一个数不用比较
     *       下标从 0 开始,所以是减二
     * @param array
     * @return
     */
    private static int[] bubbleSort(int [] array){
        for(int i = 0;i<array.length;i++){
            for(int j = 0;j <= array.length -2-i;j++){

                if(array[j] > array[j+1]){
                    int temp = array[j];
                    array[j] = array[j+1];
                    array[j+1] = temp;
                }
            }
        }
        return array;
    }
    public static void main(String[] args) {
        int[] array = {9,2,4,7,5,8,1,3,6};
        System.out.println(Arrays.toString(bubbleSort(array)));

    }
}

2. 选择排序 (SelectionSort)

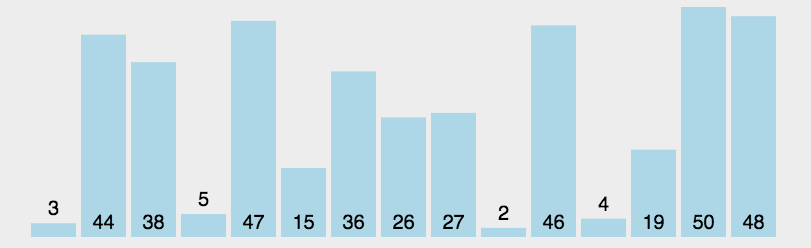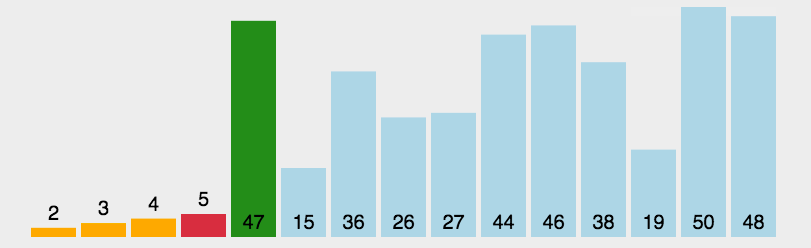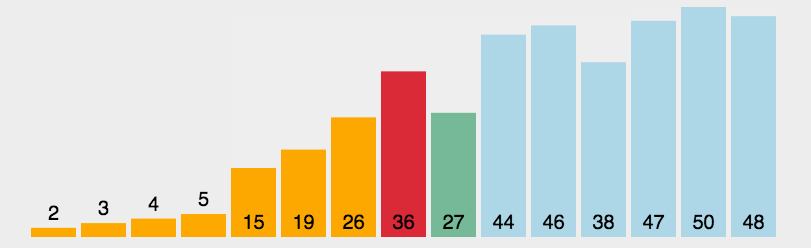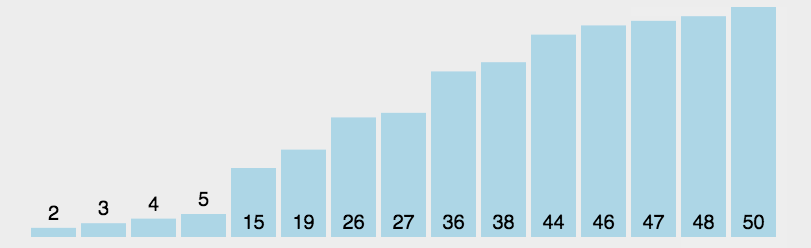
选择排序是一种简单直观的排序算法, 是减治算法的应用, 对数据不敏感, 原理是:

首先在未排序序列中找到最小元素, 存放到排列序列的起始位置, 然后在剩余未排序元素中继续寻找最小元素, 然后放到已经排好序序列的末尾, 以此类推, 直到所有元素均排序完毕

步骤:

把要排序的序列分为有序序列和无序序列
遍历序列, 每一次从无序序列找到最小元素, 定义为 minIndex=i, 放到无序序列最前面,
直到无序区间内没有元素, 也就是所有元素都排好序

动图演示:

代码展示:

package Sort;

import java.util.Arrays;

/**
 * Author:weiwei
 * description:
 * Creat:2019/5/2
 **/
public class SelectSort {

    private static int[] SelectSort(int[] array) {
        for (int i = 0; i < array.length; i++) {
            int min = i;
            for (int j = i+1; j < array.length; j++) {
                if (array[j] < array[min]) {
                    min = j;
                }
            }
            int t = array[min];
            array[min] = array[i];
            array[i] = t;

        }
        return array;
    }

    public static void main(String[] args) {
        int[] array = {8,3,7,1,4,6,2,9,5};
        System.out.println(Arrays.toString(SelectSort(array)));
    }
}

3. 插入排序 (Insertion Sort)

插入排序是一种简单直观的排序算法, 是减治算法的应用, 原理是: 通过构建有序数列, 对于未排序数据, 在已排序序列中, 从后往前扫描, 找到对应位置并插入 (每次从无序区间取一个数到有序区间去遍历, 找到插入的位置)

步骤:

从第一个元素开始, 认为第一个元素已经被排序
取出下一个元素, 在已排好序的序列中从后往前扫描
如果该元素 (已排好序) 大于新元素, 将该元素移到下一位置
重复步骤 3, 直到找到已排好序的元素小于或者等于新元素的位置
将新元素插入到该位置后
重复步骤 2-5

动图演示:

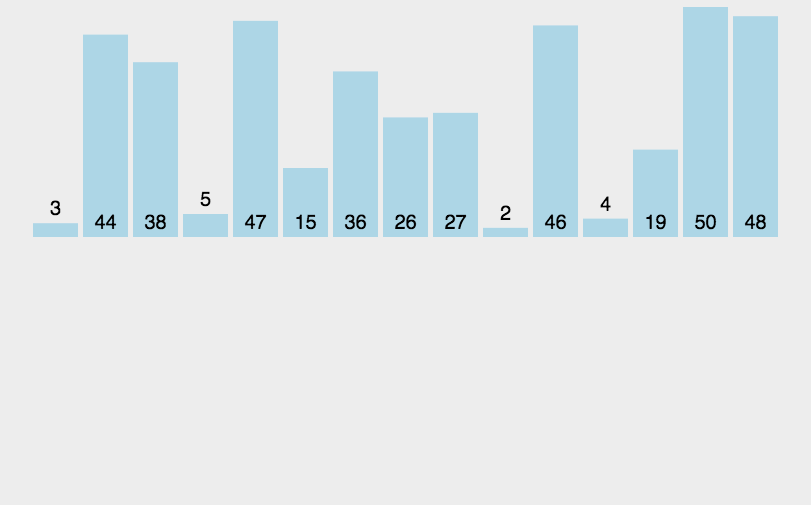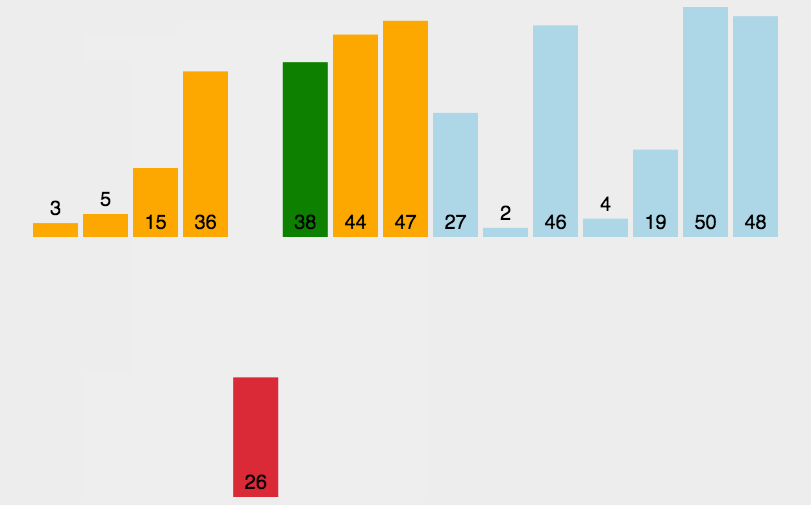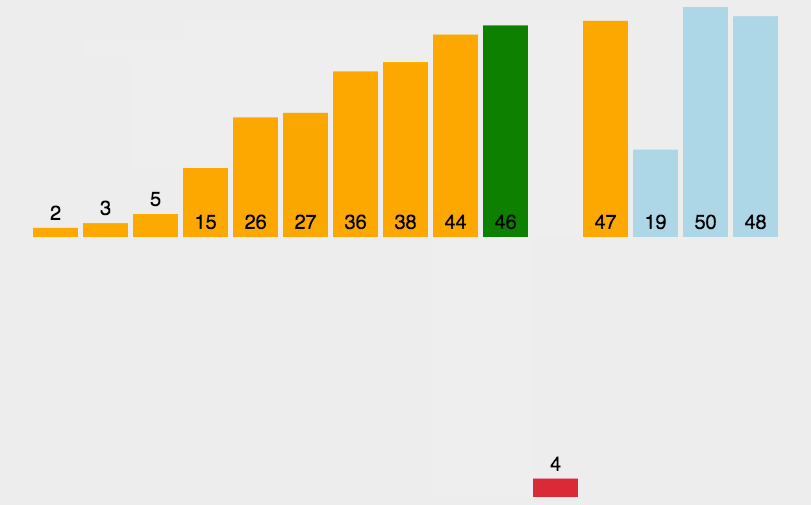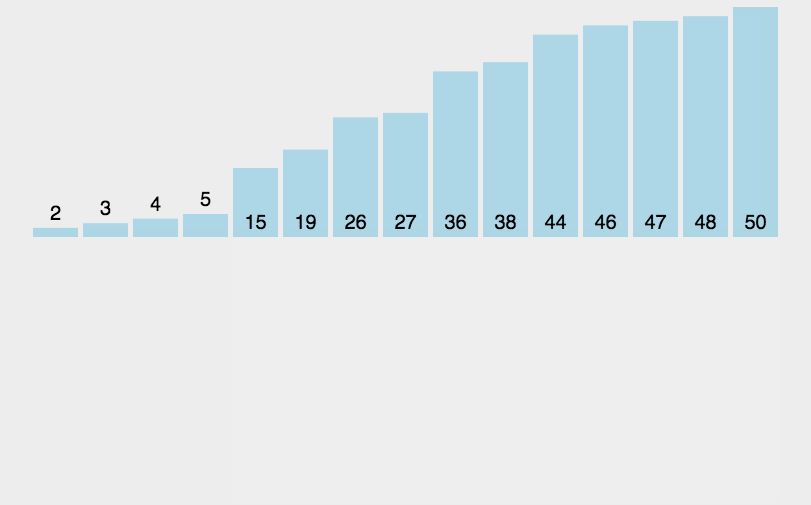
代码展示:

package Sort;

import java.util.Arrays;

/**
 * Author:weiwei
 * description:
 * Creat:2019/5/3
 **/
public class insertSort {

    /**遍历查找
     *先查找
     *再搬
     * @param array
     */
    private static void insertSort1(int[] array){
        for(int i =0;i<array.length;i++){
            //有序[0,i)
            //无序[i,array.length)
            //1.在有序区间遍历查找,从后往前查找
            int j;
            for(j=i-1;j >= 0 &&array[i] < array[j];j--){
            }
            //j+1就是要插入的位置
            //插入数据,从后往前搬数据
            int pos = j+1;
            int key = array[i];
            for( int k = i;k>pos;k--){
                array[k] = array[k-1];
            }
            array[pos] = key;
        }
    }

    /**遍历查找
     * 边查找边搬
     * @param array
     */
    private static int[] insertSort2(int[] array){
        int len = array.length;
        int preIndex,current;
        for(int i = 0;i<len;i++){
            preIndex = i-1;
            current = array[i];

            while(preIndex >= 0 && array[preIndex] > current ){
                array[preIndex+1] = array[preIndex];
                preIndex--;
            }
            array[preIndex+1] = current;
        }
        return array;
    }

    /**
     * 二分查找(重点)
     * @param array
     */
    private static void insertSort3(int[] array){
        for(int i = 0;i<array.length;i++){
            int key = array[i];
            //[0,i)
            int left = 0;
            int right = i;

            while(left < right){
                int mid = left + (left - right)/2;
                if(key == array[mid]){
                    left = mid + 1;
                }else if(key < array[mid]){
                    right = mid;
                }else{
                    left = mid +1;
                }
            }
            int pos = left;
            for (int k = i;k>pos;k--){
                array[k] = array[k-1];
            }
            array[pos] = key;
        }
    }

    public static void main(String[] args) {
        int[] array = {9,2,7,4,5,3,1,8,6,5};
        insertSort1(array);
        System.out.println(Arrays.toString(array));
    }
}

4. 希尔排序（shell sort）

希尔排序是第一个突破 O(n^2) 的排序算法，是简单插入排序的改进法，它与插入排序不同之处在于，它会提前做一个预排序, 给序列分组预排序, 也叫做分组插排, 分的组越多越接近有序

动图演示：

                ![](https://img-blog.csdnimg.cn/2019041519563662.gif)

代码展示：

package Sort;

import java.util.Arrays;

/**
 * Author:weiwei
 * description:希尔排序
 * Creat:2019/5/3
 **/
public class insertSortWithGap {

    private static void insertSortWithGap(int[] array, int gap) {
        for (int i = 0; i < array.length; i++) {
            int key = array[i];
            int j = i - gap;
            for (; j >= 0 && key < array[j]; j = j - gap) {
                array[j + gap] = array[j];
            }
            array[j + gap] = key;
        }
    }

    /**
     * 时间复杂度:
     * 最好情况:O(n)
     * 最坏情况:O(n^2)   比插排最坏情况的概率变小了
     * 平均情况:O(n^1.2 - 1.3)
     * 空间复杂度:O(1)
     * 稳定性:不稳定
     *
     * @param array
     */
    private static int[] shellSort(int[] array) {
        int gap = array.length;
        while (true) {
            //gap = gap /2;
            gap = (gap / 3) + 1;

            insertSortWithGap(array, gap);

            if (gap == 1) {
                break;
            }
        }
        return array;
    }

    public static void main(String[] args) {
        int [] array = {9,3,1,4,7,2,8,6,5};
        System.out.println(Arrays.toString(shellSort(array)));
    }
}

5. 归并排序（Merge sort）

归并排序是建立在一种建立在归并算法上一种有效的排序方法，该方法是采用分治算法的一个典型的应用，对数据不敏感, 将已有序的子序列合并，得到完全有序的序列，即先使每个子序列有序，再使子序列间有序，算法复杂度为 (nlogn)

算法描述：

把长度为 n 的序列分为两个长度为 n/2 的子序列
对这两个子序列分别归并排序
将两个排序好的子序列合并成一个最终的有序序列

动图演示：

代码展示：

package Sort;

import java.util.Arrays;

/**
 * Author:weiwei
 * description:归并排序(递归方式)
 * Creat:2019/4/27
 **/
public class MergeSort {
    private static void merge(int[] array,int low,int mid,int high,int[] extra){
        int i = low;  //遍历[low,mid]
        int j = mid;  //遍历[mid,high]
        int x = 0;    //遍历extra

        while(i < mid && j < high){
             if(array[i] <= array[j]){
                 extra[x++] = array[i++];
             }else{
                 extra[x++] = array[j++];
             }
        }
        while(i < mid){
            extra[x++] = array[i++];
        }
        while(j < high){
            extra[x++] = array[j++];
        }
        for(int k = low;k < high;k++){
            array[k] = extra[k - low];
        }
    }
    private static void mergeSortInner(int[] array,int low,int high,int[] extra){
        if (low == high - 1){
            return;
        }
        if(low >= high){
            return;
        }

        //平均切分
        int mid = low + (high - low)/2;
        //[low,mid)+[mid,high)
        //2.分治算法处理两个小区间
        mergeSortInner(array,low,mid,extra);
        mergeSortInner(array,mid,high,extra);

        //左右两个小区间已经有序了
        merge(array,low,mid,high,extra);
    }

    private static void mergeSort(int[] array) {
        int[] extra = new int [array.length];//设定长度,避免造成空间浪费
        mergeSortInner(array,0,array.length,extra);
    }

    //非递归方式
    private static void mergeNoR(int[] array){
        int[] extra = new int [array.length];
        for(int i = 1;i<array.length;i *= 2){
            for(int j =0;j<array.length;j +=2 * i){
                int low = j;
                int mid = low + i;
                if( mid >= array.length){
                    continue;
                }
                int high = mid + i;
                if(high > array.length){
                    high = array.length;
                }
                merge(array,low,mid,high,extra);
            }
        }
    }

    public static void main(String[] args) {
        int[] array1 = {9,3,1,5,4,2,7,6,8};
        int[] array2 = {8,3,1,2,5,3,7,6,2};
        mergeSort(array1);
        mergeNoR(array2);
        System.out.println(Arrays.toString(array1));
        System.out.println(Arrays.toString(array2));
    }
}

6. 快速排序 (Quick Sort)

快速排序的基本思想：

    在要排序的序列中选择一个基准值 (通常选择最右边的值为基准值), 然后遍历整个序列, 每个数都和基准值进行比较, 并且发生一定的交换, 遍历结束后使得比基准值小的数(包括等于) 都在基准值的左边, 比基准值大的数 (包括等于) 都在基准值的右边, 然后采用分治算法的思想, 分别对两个小的区间进行同样的方式处理, 直到区间的 size=0 或者 = 1, 就说明序列已经有序了, 快速排序完成

算法描述:

快速排序使用分治算法来把一个序列分为两个子序列, 具体算法描述如下：

从序列中选择最右边的数作为基准, 称为 “基准值”（pivot）；
遍历排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；
```
 ![](https://img-blog.csdnimg.cn/2019050416332747.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80MzIyNDUzOQ==,size_16,color_FFFFFF,t_70)  
```
递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。

快速排序的步骤:

选择基准值 (选择基准值有三个方法)

选择最边上作为基准值 (左右都可以)
随机法 (random.nextInt())
三数取中法 [对于第二三中方法, 确定基准值后, 将基准值交换到最边上]

分割 (partition 操作), 比基准值 <= 在基准值左边, 比基准值 >= 在基准值右边, partition 操作也有三种方法:

Hover 法 (左右遍历)
挖坑法 (左右遍历)
前后下标法 (前后遍历)

用分治法处理左右两个小区间, 直到区间的 size == 1(已经有序) 或者 size == 0, 则停止排序动态图展示:

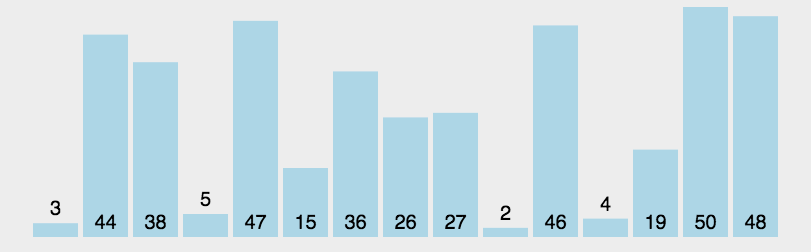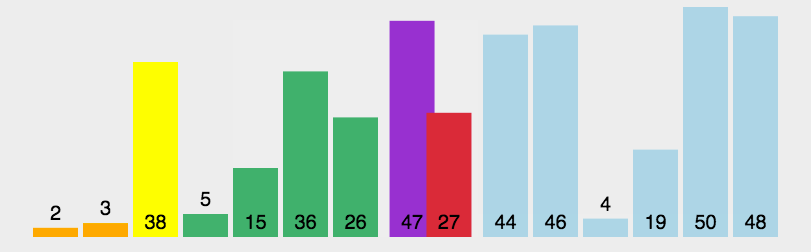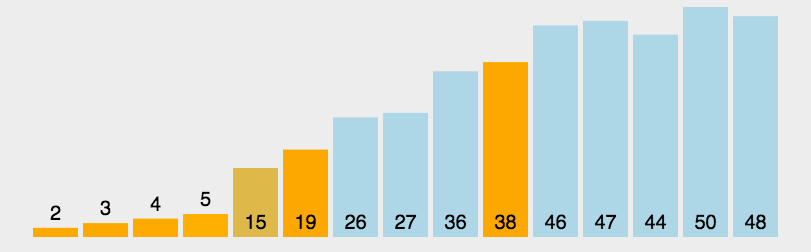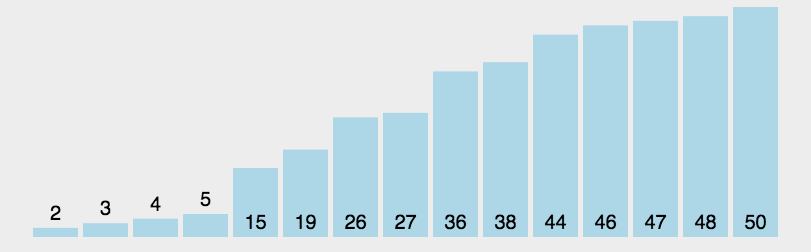
代码展示:

快速排序

package Sort;

import java.util.Arrays;

/**
 * Author:weiwei
 * description:快速排序
 * Creat:2019/4/27
 **/
public class QuickSort {

    private static void swap(int[] array,int i,int j){
        int t = array[i];
        array[i] = array[j];
        array[j] = t;
    }

    private static int  partition1(int[] array,int left,int right){
        int begin = left;
        int end = right;
        int pivot = array[right];
        while(begin < end){
            while( begin < end && array[begin] <= pivot){
                begin++;  //当前数比基准值小,就往后遍历,遇到比基准值大的数才停下来
            }
            while(begin < end && array[end] >= pivot){
                end--;    //当前数比基准值大,就往前遍历,遇到比基准值小的数才停下来
            }
            swap(array,begin,end); //否则,遍历无法继续,交换所指向的值,再继续遍历
        }
        swap(array,begin,right);  //遍历到最后begin == end,将right的值与begin的值交换
        return begin;             //此时,序列中基准值左边所有的值就比基准值小,右边的数就比基准值大

    }
private static void quickSortInner(int[] array,int left,int right){
        if(left > right){
            //size == 1 已经有序
            return;
        }
        if(left == right){
            //size == 0
            return;
        }
        int originIndex = medianofthree(array,left,right);
        swap(array,originIndex,right);

        //要排序的区间是array[left,right]
        //1.找基准值 array[right]
        //2.遍历整个区间,把区间的为三部分
        int pivotIndex = partition1(array,left,right);
        //3.分治算法
        //用相同的方式处理两个小区间,直到size == 1 | size == 0
        //比基准值小的区间[left,pivotIndex-1]
        quickSortInner(array,left,pivotIndex-1);
        //比基准值大的区间[pivotIndex+1,right]
        quickSortInner(array,pivotIndex+1,right);
    }
    private static void  quickSort(int[] array){
        quickSortInner(array,0,array.length -1);
    }

    public static void main(String[] args) {
        int[] array = {9,3,1,5,4,2,7,6,8};
        quickSort(array);
        System.out.println(Arrays.toString(array));
    }
}

用 Hover 方法进行 partition 操作

//Hover法做partition操作
    private static int  partition1(int[] array,int left,int right){
        int begin = left;
        int end = right;
        int pivot = array[right];
        while(begin < end){
            while( begin < end && array[begin] <= pivot){
                begin++;  //当前数比基准值小,就往后遍历,遇到比基准值大的数才停下来
            }
            while(begin < end && array[end] >= pivot){
                end--;    //当前数比基准值大,就往前遍历,遇到比基准值小的数才停下来
            }
            swap(array,begin,end); //否则,遍历无法继续,交换所指向的值,再继续遍历
        }
        swap(array,begin,right);  //遍历到最后begin == end,将right的值与begin的值交换
        return begin;             //此时,序列中基准值左边所有的值就比基准值小,右边的数就比基准值大

    }

用挖坑法做 partition 操作

//用挖坑法做partition操作
    private static int partition2(int[] array,int left,int right){
        int begin = left;
        int end = right;
        int pivot = array[right];
        while(begin < end){
            while(begin < end && array[begin] <= pivot){
                begin++;   //当前数比基准值小,就往后遍历,遇到比基准值大的数才停下来
            }
            array[begin] = array[end];  //否则,将end的值赋给begin
            while(begin < end && array[begin] <= pivot){
                end--;    //当前数比基准值大,就往前遍历,遇到比基准值小的数才停下来
            }
            array[end] = array[begin]; //否则,将begin的值赋给end
        }
        array[begin] = pivot;  //最终begin == end时,将pivot的值赋给begin
        return begin;
    }

用前后遍历的方法 partition 操作

//前后下标法做partition操作
    private static int parttiton3(int[] array,int left,int right){
        int d = left;
        for(int i = left;i<right;i++){
            if(array[i] < array[right]){
                swap(array,d,i);
                d++;
            }
        }
        swap(array,d,right);
        return d;
    }

选择基准的方法: 三数取中法

//三数取中
    private static int medianofthree(int[] array,int left,int right) {
        int mid = left + (right - left) / 2;
        if (array[left] > array[right]) {
            if (array[left] < array[mid]) {
                return left;
            } else if (array[mid] > array[right]) {
                return mid;
            } else {
                return right;
            }
        } else {
            if (array[right] < array[mid]) {
                return right;
            } else if (array[mid] > array[left]) {
                return mid;
            } else {
                return left;
            }
        }
    }

7. 堆排序 (Heap Sort)

堆排序（Heapsort）是指利用堆这种数据结构所设计的一种排序算法。是减治算法的应用, 对数据不敏感, 堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。

算法描述

 1. 将初始待排序关键字序列构建成大堆，此堆为初始的无序区；  
 2. 选择最大的元素 (堆顶元素) 放到无序序列最后面，此时得到新的无序区和新的有序区, 每次在无序序列中选择最大的的元素放到无序序列最后面,  
 3. 直到最后叶子结点, 不再向下调整, 堆排序完成

动态图演示:

                                  ![](https://img-blog.csdnimg.cn/20190421095934922.gif)

代码展示:

package com.bittech;

/**
 * Author:weiwei
 * description:堆排序
 * Creat:2019/4/27
 **/
public class heapSort {

    private static void heapify(int[] array,int size,int index){
        //判断index是不是叶子结点
        while(2*index+1 < size){
            //找到最大孩子的下标
            int max = 2 * index + 1;
            if(max + 1 <size && array[max+1] > array[max]){
                max = 2 * index + 2;
            }

            //3.判断最大得孩子和根的值
            if(array[index] < array[max]){
                swap(array,index,max);

                index = max;
            }else{
                //根的值比较大,不需要交换,可以直接退出了
                break;
            }
        }
    }
    private static void createHeap(int[] array){
        //[从最后一个非叶子节点的下标,根]  向下调整
        //[(array.length-2)/2,0]
        for(int i = (array.length-2/2);i>=0;i--){
            heapify(array,array.length,i);
        }
    }
    private static void swap(int[] array,int i,int j){
        int t =array[i];
        array[i] = array[j];
        array[j] = t;

    }
    private static void heapSort(int[] array){
        //建堆  大堆
        createHeap(array);

        //减治处理
        for(int i =0;i<array.length;i++){
            //有序[length - i,length]
            //无序[0,length - i - 1]
            //最大的数在[0],最大的数应该放到的下标是
            //[length-i-1]
            swap(array,0,array.length -1-i);
            //处理[0]无序剩余部分满足堆的性质
            //无序[0,length-i-2]
            //有序[length-i-1,length]
            //size剩余无序部分的长度
            heapify(array,array.length-1-i,0);
        }
    }

    public static void main(String[] args) {
        int[] array = { 9, 5, 2, 7, 3, 6, 8, 8, 4, 9, 3, 1, 2 };
        heapSort(array);
        for (int item: array) {
            System.out.print(item + " ");
        }
        System.out.println();
    }
}

七大经典排序算法

1. 冒泡排序 (BubbleSort)

2. 选择排序 (SelectionSort)

3. 插入排序 (Insertion Sort)

4. 希尔排序（shell sort）

5. 归并排序（Merge sort）

6. 快速排序 (Quick Sort)

7. 堆排序 (Heap Sort)